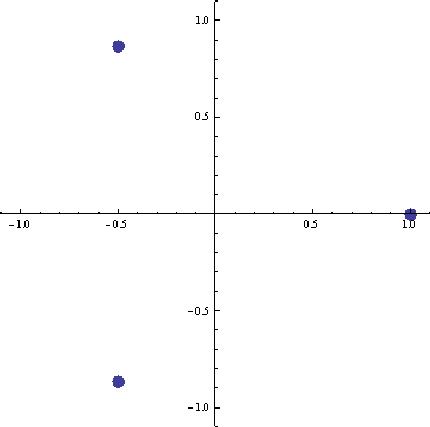
Finding & graphing the cube roots of 1, or solving the equation x³=1, using Mathematica

NSolve[x^{^}3'1,x]

{{x' -0.5 - 0.866025 '},{x' -0.5 +0.866025 '},{x'1.}}

{{x->Cos[4*p/3] + '*Sin[4*p/3]},{x->Cos[2*p/3] + '*Sin[2*p/3]},x->Cos[0*p/3] + '*Sin[0*p/3]}

{{x->{x' '^('*4*p/3)},{x' '^('*2*p/3),{x' '^('*0*p/3)}}

Note: '^('*4*p/3) = -0.5 - 0.866025 '  because, '^('x) = cos x + ' sin x  

(see  binomial expansion to get e^ix )

ListPlot[Map[{Re[#],Im[#]}&,x/.Solve[x^3'1]],PlotRange'1.1,AspectRatio'Automatic,

PlotStyle'PointSize[0.03]]

Notice the solutions are on a circle of radius 1, 120^o  apart.

^{Solve: x5 = 2 - 2*'*Sqrt(3) or find the 5 - fifth roots of 2 - 2*'*Sqrt(3)} 

See also points on the spiral (1+i)ⁿ